PINE LIBRARY
Atualizado math
Library "math"
It's a library of discrete aproximations of a price or Series float it uses Fourier Discrete transform, Laplace Discrete Original and Modified transform and Euler's Theoreum for Homogenus White noice operations. Calling functions without source value it automatically take close as the default source value.
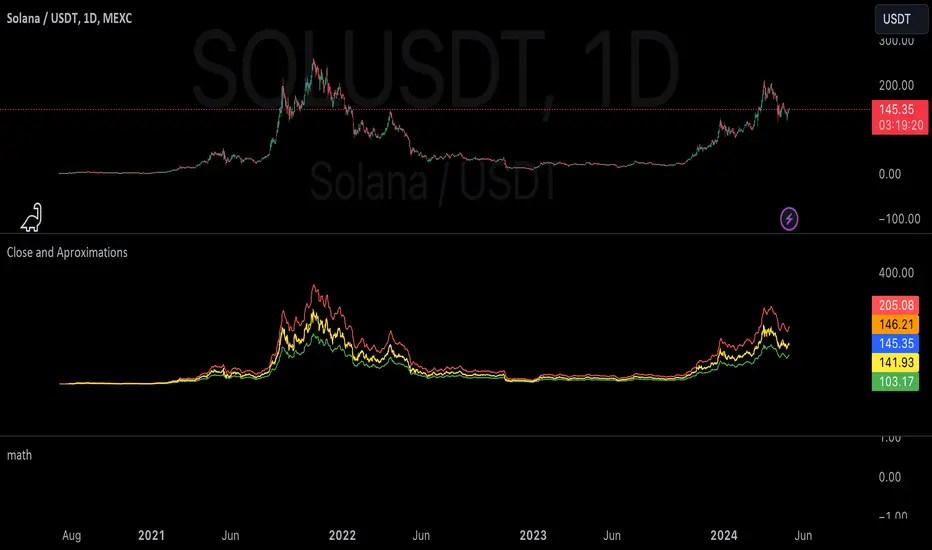
Here is a picture of Laplace and Fourier approximated close prices from this library:

Copy this indicator and try it yourself:
Pine Script®
DFT3(xval, _dir)
Discrete Fourier Transform with last 3 points
Parameters:
xval (float): Source series
_dir (int): Direction parameter
Returns: Aproxiated source value
DFT2(xval, _dir)
Discrete Fourier Transform with last 2 points
Parameters:
xval (float): Source series
_dir (int): Direction parameter
Returns: Aproxiated source value
FFT(xval)
Fast Fourier Transform once. It aproximates usig last 3 points.
Parameters:
xval (float): Source series
Returns: Aproxiated source value
DFT32(xval)
Combined Discrete Fourier Transforms of DFT3 and DTF2 it aproximates last point by first
aproximating last 3 ponts and than using last 2 points of the previus.
Parameters:
xval (float): Source series
Returns: Aproxiated source value
DTF32(xval)
Combined Discrete Fourier Transforms of DFT3 and DTF2 it aproximates last point by first
aproximating last 3 ponts and than using last 2 points of the previus.
Parameters:
xval (float): Source series
Returns: Aproxiated source value
LFT3(xval, _dir, a)
Discrete Laplace Transform with last 3 points
Parameters:
xval (float): Source series
_dir (int): Direction parameter
a (float): laplace coeficient
Returns: Aproxiated source value
LFT2(xval, _dir, a)
Discrete Laplace Transform with last 2 points
Parameters:
xval (float): Source series
_dir (int): Direction parameter
a (float): laplace coeficient
Returns: Aproxiated source value
LFT(xval, a)
Fast Laplace Transform once. It aproximates usig last 3 points.
Parameters:
xval (float): Source series
a (float): laplace coeficient
Returns: Aproxiated source value
LFT32(xval, a)
Combined Discrete Laplace Transforms of LFT3 and LTF2 it aproximates last point by first
aproximating last 3 ponts and than using last 2 points of the previus.
Parameters:
xval (float): Source series
a (float): laplace coeficient
Returns: Aproxiated source value
LTF32(xval, a)
Combined Discrete Laplace Transforms of LFT3 and LTF2 it aproximates last point by first
aproximating last 3 ponts and than using last 2 points of the previus.
Parameters:
xval (float): Source series
a (float): laplace coeficient
Returns: Aproxiated source value
whitenoise(indic_, _devided, minEmaLength, maxEmaLength, src)
Ehler's Universal Oscillator with White Noise, without extra aproximated src.
It uses dinamic EMA to aproximate indicator and thus reducing noise.
Parameters:
indic_ (float): Input series for the indicator values to be smoothed
_devided (int): Divisor for oscillator calculations
minEmaLength (int): Minimum EMA length
maxEmaLength (int): Maximum EMA length
src (float): Source series
Returns: Smoothed indicator value
whitenoise(indic_, dft1, _devided, minEmaLength, maxEmaLength, src)
Ehler's Universal Oscillator with White Noise and DFT1.
It uses src and sproxiated src (dft1) to clearly define white noice.
It uses dinamic EMA to aproximate indicator and thus reducing noise.
Parameters:
indic_ (float): Input series for the indicator values to be smoothed
dft1 (float): Aproximated src value for white noice calculation
_devided (int): Divisor for oscillator calculations
minEmaLength (int): Minimum EMA length
maxEmaLength (int): Maximum EMA length
src (float): Source series
Returns: Smoothed indicator value
smooth(dft1, indic__, _devided, minEmaLength, maxEmaLength, src)
Smoothing source value with help of indicator series and aproximated source value
It uses src and sproxiated src (dft1) to clearly define white noice.
It uses dinamic EMA to aproximate src and thus reducing noise.
Parameters:
dft1 (float): Value to be smoothed.
indic__ (float): Optional input for indicator to help smooth dft1 (default is FFT)
_devided (int): Divisor for smoothing calculations
minEmaLength (int): Minimum EMA length
maxEmaLength (int): Maximum EMA length
src (float): Source series
Returns: Smoothed source (src) series
smooth(indic__, _devided, minEmaLength, maxEmaLength, src)
Smoothing source value with help of indicator series
It uses dinamic EMA to aproximate src and thus reducing noise.
Parameters:
indic__ (float): Optional input for indicator to help smooth dft1 (default is FFT)
_devided (int): Divisor for smoothing calculations
minEmaLength (int): Minimum EMA length
maxEmaLength (int): Maximum EMA length
src (float): Source series
Returns: Smoothed src series
vzo_ema(src, len)
Volume Zone Oscillator with EMA smoothing
Parameters:
src (float): Source series
len (simple int): Length parameter for EMA
Returns: VZO value
vzo_sma(src, len)
Volume Zone Oscillator with SMA smoothing
Parameters:
src (float): Source series
len (int): Length parameter for SMA
Returns: VZO value
vzo_wma(src, len)
Volume Zone Oscillator with WMA smoothing
Parameters:
src (float): Source series
len (int): Length parameter for WMA
Returns: VZO value
alma2(series, windowsize, offset, sigma)
Arnaud Legoux Moving Average 2 accepts sigma as series float
Parameters:
series (float): Input series
windowsize (int): Size of the moving average window
offset (float): Offset parameter
sigma (float): Sigma parameter
Returns: ALMA value
Wavelet(src, len, offset, sigma)
Aproxiates srt using Discrete wavelet transform.
Parameters:
src (float): Source series
len (int): Length parameter for ALMA
offset (simple float)
sigma (simple float)
Returns: Wavelet-transformed series
Wavelet_std(src, len, offset, mag)
Aproxiates srt using Discrete wavelet transform with standard deviation as a magnitude.
Parameters:
src (float): Source series
len (int): Length parameter for ALMA
offset (float): Offset parameter for ALMA
mag (int): Magnitude parameter for standard deviation
Returns: Wavelet-transformed series
LaplaceTransform(xval, N, a)
Original Laplace Transform over N set of close prices
Parameters:
xval (float): series to aproximate
N (int): number of close prices in calculations
a (float): laplace coeficient
Returns: Aproxiated source value
NLaplaceTransform(xval, N, a, repeat)
Y repetirions on Original Laplace Transform over N set of close prices, each time N-k set of close prices
Parameters:
xval (float): series to aproximate
N (int): number of close prices in calculations
a (float): laplace coeficient
repeat (int): number of repetitions
Returns: Aproxiated source value
LaplaceTransformsum(xval, N, a, b)
Sum of 2 exponent coeficient of Laplace Transform over N set of close prices
Parameters:
xval (float): series to aproximate
N (int): number of close prices in calculations
a (float): laplace coeficient
b (float): second laplace coeficient
Returns: Aproxiated source value
NLaplaceTransformdiff(xval, N, a, b, repeat)
Difference of 2 exponent coeficient of Laplace Transform over N set of close prices
Parameters:
xval (float): series to aproximate
N (int): number of close prices in calculations
a (float): laplace coeficient
b (float): second laplace coeficient
repeat (int): number of repetitions
Returns: Aproxiated source value
N_divLaplaceTransformdiff(xval, N, a, b, repeat)
N repetitions of Difference of 2 exponent coeficient of Laplace Transform over N set of close prices, with dynamic rotation
Parameters:
xval (float): series to aproximate
N (int): number of close prices in calculations
a (float): laplace coeficient
b (float): second laplace coeficient
repeat (int): number of repetitions
Returns: Aproxiated source value
LaplaceTransformdiff(xval, N, a, b)
Difference of 2 exponent coeficient of Laplace Transform over N set of close prices
Parameters:
xval (float): series to aproximate
N (int): number of close prices in calculations
a (float): laplace coeficient
b (float): second laplace coeficient
Returns: Aproxiated source value
NLaplaceTransformdiffFrom2(xval, N, a, b, repeat)
N repetitions of Difference of 2 exponent coeficient of Laplace Transform over N set of close prices, second element has for 1 higher exponent factor
Parameters:
xval (float): series to aproximate
N (int): number of close prices in calculations
a (float): laplace coeficient
b (float): second laplace coeficient
repeat (int): number of repetitions
Returns: Aproxiated source value
N_divLaplaceTransformdiffFrom2(xval, N, a, b, repeat)
N repetitions of Difference of 2 exponent coeficient of Laplace Transform over N set of close prices, second element has for 1 higher exponent factor, dynamic rotation
Parameters:
xval (float): series to aproximate
N (int): number of close prices in calculations
a (float): laplace coeficient
b (float): second laplace coeficient
repeat (int): number of repetitions
Returns: Aproxiated source value
LaplaceTransformdiffFrom2(xval, N, a, b)
Difference of 2 exponent coeficient of Laplace Transform over N set of close prices, second element has for 1 higher exponent factor
Parameters:
xval (float): series to aproximate
N (int): number of close prices in calculations
a (float): laplace coeficient
b (float): second laplace coeficient
Returns: Aproxiated source value
It's a library of discrete aproximations of a price or Series float it uses Fourier Discrete transform, Laplace Discrete Original and Modified transform and Euler's Theoreum for Homogenus White noice operations. Calling functions without source value it automatically take close as the default source value.
Here is a picture of Laplace and Fourier approximated close prices from this library:
Copy this indicator and try it yourself:
import AutomatedTradingAlgorithms/math/1 as math
//@version=5
indicator("Close Price with Aproximations", shorttitle="Close and Aproximations", overlay=false)
// Sample input data (replace this with your own data)
inputData = close
// Plot Close Price
plot(inputData, color=color.blue, title="Close Price")
ltf32_result = math.LTF32(a=0.01)
plot(ltf32_result, color=color.green, title="LTF32 Aproximation")
fft_result = math.FFT()
plot(fft_result, color=color.red, title="Fourier Aproximation")
wavelet_result = math.Wavelet()
plot(wavelet_result, color=color.orange, title="Wavelet Aproximation")
wavelet_std_result = math.Wavelet_std()
plot(wavelet_std_result, color=color.yellow, title="Wavelet_std Aproximation")
DFT3(xval, _dir)
Discrete Fourier Transform with last 3 points
Parameters:
xval (float): Source series
_dir (int): Direction parameter
Returns: Aproxiated source value
DFT2(xval, _dir)
Discrete Fourier Transform with last 2 points
Parameters:
xval (float): Source series
_dir (int): Direction parameter
Returns: Aproxiated source value
FFT(xval)
Fast Fourier Transform once. It aproximates usig last 3 points.
Parameters:
xval (float): Source series
Returns: Aproxiated source value
DFT32(xval)
Combined Discrete Fourier Transforms of DFT3 and DTF2 it aproximates last point by first
aproximating last 3 ponts and than using last 2 points of the previus.
Parameters:
xval (float): Source series
Returns: Aproxiated source value
DTF32(xval)
Combined Discrete Fourier Transforms of DFT3 and DTF2 it aproximates last point by first
aproximating last 3 ponts and than using last 2 points of the previus.
Parameters:
xval (float): Source series
Returns: Aproxiated source value
LFT3(xval, _dir, a)
Discrete Laplace Transform with last 3 points
Parameters:
xval (float): Source series
_dir (int): Direction parameter
a (float): laplace coeficient
Returns: Aproxiated source value
LFT2(xval, _dir, a)
Discrete Laplace Transform with last 2 points
Parameters:
xval (float): Source series
_dir (int): Direction parameter
a (float): laplace coeficient
Returns: Aproxiated source value
LFT(xval, a)
Fast Laplace Transform once. It aproximates usig last 3 points.
Parameters:
xval (float): Source series
a (float): laplace coeficient
Returns: Aproxiated source value
LFT32(xval, a)
Combined Discrete Laplace Transforms of LFT3 and LTF2 it aproximates last point by first
aproximating last 3 ponts and than using last 2 points of the previus.
Parameters:
xval (float): Source series
a (float): laplace coeficient
Returns: Aproxiated source value
LTF32(xval, a)
Combined Discrete Laplace Transforms of LFT3 and LTF2 it aproximates last point by first
aproximating last 3 ponts and than using last 2 points of the previus.
Parameters:
xval (float): Source series
a (float): laplace coeficient
Returns: Aproxiated source value
whitenoise(indic_, _devided, minEmaLength, maxEmaLength, src)
Ehler's Universal Oscillator with White Noise, without extra aproximated src.
It uses dinamic EMA to aproximate indicator and thus reducing noise.
Parameters:
indic_ (float): Input series for the indicator values to be smoothed
_devided (int): Divisor for oscillator calculations
minEmaLength (int): Minimum EMA length
maxEmaLength (int): Maximum EMA length
src (float): Source series
Returns: Smoothed indicator value
whitenoise(indic_, dft1, _devided, minEmaLength, maxEmaLength, src)
Ehler's Universal Oscillator with White Noise and DFT1.
It uses src and sproxiated src (dft1) to clearly define white noice.
It uses dinamic EMA to aproximate indicator and thus reducing noise.
Parameters:
indic_ (float): Input series for the indicator values to be smoothed
dft1 (float): Aproximated src value for white noice calculation
_devided (int): Divisor for oscillator calculations
minEmaLength (int): Minimum EMA length
maxEmaLength (int): Maximum EMA length
src (float): Source series
Returns: Smoothed indicator value
smooth(dft1, indic__, _devided, minEmaLength, maxEmaLength, src)
Smoothing source value with help of indicator series and aproximated source value
It uses src and sproxiated src (dft1) to clearly define white noice.
It uses dinamic EMA to aproximate src and thus reducing noise.
Parameters:
dft1 (float): Value to be smoothed.
indic__ (float): Optional input for indicator to help smooth dft1 (default is FFT)
_devided (int): Divisor for smoothing calculations
minEmaLength (int): Minimum EMA length
maxEmaLength (int): Maximum EMA length
src (float): Source series
Returns: Smoothed source (src) series
smooth(indic__, _devided, minEmaLength, maxEmaLength, src)
Smoothing source value with help of indicator series
It uses dinamic EMA to aproximate src and thus reducing noise.
Parameters:
indic__ (float): Optional input for indicator to help smooth dft1 (default is FFT)
_devided (int): Divisor for smoothing calculations
minEmaLength (int): Minimum EMA length
maxEmaLength (int): Maximum EMA length
src (float): Source series
Returns: Smoothed src series
vzo_ema(src, len)
Volume Zone Oscillator with EMA smoothing
Parameters:
src (float): Source series
len (simple int): Length parameter for EMA
Returns: VZO value
vzo_sma(src, len)
Volume Zone Oscillator with SMA smoothing
Parameters:
src (float): Source series
len (int): Length parameter for SMA
Returns: VZO value
vzo_wma(src, len)
Volume Zone Oscillator with WMA smoothing
Parameters:
src (float): Source series
len (int): Length parameter for WMA
Returns: VZO value
alma2(series, windowsize, offset, sigma)
Arnaud Legoux Moving Average 2 accepts sigma as series float
Parameters:
series (float): Input series
windowsize (int): Size of the moving average window
offset (float): Offset parameter
sigma (float): Sigma parameter
Returns: ALMA value
Wavelet(src, len, offset, sigma)
Aproxiates srt using Discrete wavelet transform.
Parameters:
src (float): Source series
len (int): Length parameter for ALMA
offset (simple float)
sigma (simple float)
Returns: Wavelet-transformed series
Wavelet_std(src, len, offset, mag)
Aproxiates srt using Discrete wavelet transform with standard deviation as a magnitude.
Parameters:
src (float): Source series
len (int): Length parameter for ALMA
offset (float): Offset parameter for ALMA
mag (int): Magnitude parameter for standard deviation
Returns: Wavelet-transformed series
LaplaceTransform(xval, N, a)
Original Laplace Transform over N set of close prices
Parameters:
xval (float): series to aproximate
N (int): number of close prices in calculations
a (float): laplace coeficient
Returns: Aproxiated source value
NLaplaceTransform(xval, N, a, repeat)
Y repetirions on Original Laplace Transform over N set of close prices, each time N-k set of close prices
Parameters:
xval (float): series to aproximate
N (int): number of close prices in calculations
a (float): laplace coeficient
repeat (int): number of repetitions
Returns: Aproxiated source value
LaplaceTransformsum(xval, N, a, b)
Sum of 2 exponent coeficient of Laplace Transform over N set of close prices
Parameters:
xval (float): series to aproximate
N (int): number of close prices in calculations
a (float): laplace coeficient
b (float): second laplace coeficient
Returns: Aproxiated source value
NLaplaceTransformdiff(xval, N, a, b, repeat)
Difference of 2 exponent coeficient of Laplace Transform over N set of close prices
Parameters:
xval (float): series to aproximate
N (int): number of close prices in calculations
a (float): laplace coeficient
b (float): second laplace coeficient
repeat (int): number of repetitions
Returns: Aproxiated source value
N_divLaplaceTransformdiff(xval, N, a, b, repeat)
N repetitions of Difference of 2 exponent coeficient of Laplace Transform over N set of close prices, with dynamic rotation
Parameters:
xval (float): series to aproximate
N (int): number of close prices in calculations
a (float): laplace coeficient
b (float): second laplace coeficient
repeat (int): number of repetitions
Returns: Aproxiated source value
LaplaceTransformdiff(xval, N, a, b)
Difference of 2 exponent coeficient of Laplace Transform over N set of close prices
Parameters:
xval (float): series to aproximate
N (int): number of close prices in calculations
a (float): laplace coeficient
b (float): second laplace coeficient
Returns: Aproxiated source value
NLaplaceTransformdiffFrom2(xval, N, a, b, repeat)
N repetitions of Difference of 2 exponent coeficient of Laplace Transform over N set of close prices, second element has for 1 higher exponent factor
Parameters:
xval (float): series to aproximate
N (int): number of close prices in calculations
a (float): laplace coeficient
b (float): second laplace coeficient
repeat (int): number of repetitions
Returns: Aproxiated source value
N_divLaplaceTransformdiffFrom2(xval, N, a, b, repeat)
N repetitions of Difference of 2 exponent coeficient of Laplace Transform over N set of close prices, second element has for 1 higher exponent factor, dynamic rotation
Parameters:
xval (float): series to aproximate
N (int): number of close prices in calculations
a (float): laplace coeficient
b (float): second laplace coeficient
repeat (int): number of repetitions
Returns: Aproxiated source value
LaplaceTransformdiffFrom2(xval, N, a, b)
Difference of 2 exponent coeficient of Laplace Transform over N set of close prices, second element has for 1 higher exponent factor
Parameters:
xval (float): series to aproximate
N (int): number of close prices in calculations
a (float): laplace coeficient
b (float): second laplace coeficient
Returns: Aproxiated source value
Notas de Lançamento
v2Added:
calculateParameters(src, n)
calculateParameter: aproximates parrameters for a * e^k + b * e^l
Parameters:
src (float): series price Source
n (int)
Returns: a k b l parameters for a * e^k + b * e^l
LaplaceTransformv1(xval, N, a, b, c, d, repeat)
LaplaceTransformv1: My version 1 of laplace transform with 4 parrameters
Parameters:
xval (float): series to aproximate
N (int): number of close prices in calculations
a (float): laplace coeficient
b (float): second laplace coeficient
c (float): laplace multyply
d (float): second laplace multiply
repeat (int): number of repetitions
Returns: Aproxiated source value
LaplaceTransformv2(xval, N, a, b, c, d, repeat)
LaplaceTransformv1: My version 1 of laplace transform with 4 parrameters
Parameters:
xval (float): series to aproximate
N (int): number of close prices in calculations
a (float): laplace coeficient
b (float): second laplace coeficient
c (float): laplace multyply
d (float): second laplace multiply
repeat (int): number of repetitions
Returns: Aproxiated source value
Notas de Lançamento
added Laplace-Stieltjes transformNotas de Lançamento
v4Added:
LaplaceTransformv3(xval, N, a, b, c, d, repeat)
LaplaceTransformv3: My version 3 of laplace transform with 4 parrameters
Parameters:
xval (float): series to aproximate
N (int): number of close prices in calculations
a (float): laplace coeficient
b (float): second laplace coeficient
c (float): laplace multyply
d (float): second laplace multiply
repeat (int): number of repetitions
Returns: Aproxiated source value
LaplaceStieltjesTransform(xval, N, a, b, c, d, repeat)
LaplaceStieltjesTransform: Laplace Stieltjes Transform with 4 parrameters
Parameters:
xval (float): series to aproximate
N (int): number of close prices in calculations
a (float): laplace coeficient
b (float): second laplace coeficient
c (float): laplace multyply
d (float): second laplace multiply
repeat (int): number of repetitions
Returns: Aproxiated source value
Biblioteca do Pine
Em verdadeiro espírito TradingView, o autor publicou este código Pine como uma biblioteca de código aberto para que outros programadores Pine da nossa comunidade possam reutilizá-lo. Parabéns ao autor! Você pode usar esta biblioteca de forma privada ou em outras publicações de código aberto, mas a reutilização deste código em publicações é regida pelas Regras da Casa.
Automated Trading Algorithms: discord.gg/xuKHyhPKS6
Tutorials-YouTube: youtube.com/channel/UCJH8wJ8Ab_O-HTb0wrrtAKQ
Mathematical papers:
algoalert.net/pdfs/fourier.pdf
algoalert.net/pdfs/IEEEwavelet.pdf
Tutorials-YouTube: youtube.com/channel/UCJH8wJ8Ab_O-HTb0wrrtAKQ
Mathematical papers:
algoalert.net/pdfs/fourier.pdf
algoalert.net/pdfs/IEEEwavelet.pdf
Aviso legal
As informações e publicações não se destinam a ser, e não constituem, conselhos ou recomendações financeiras, de investimento, comerciais ou de outro tipo fornecidos ou endossados pela TradingView. Leia mais nos Termos de Uso.
Biblioteca do Pine
Em verdadeiro espírito TradingView, o autor publicou este código Pine como uma biblioteca de código aberto para que outros programadores Pine da nossa comunidade possam reutilizá-lo. Parabéns ao autor! Você pode usar esta biblioteca de forma privada ou em outras publicações de código aberto, mas a reutilização deste código em publicações é regida pelas Regras da Casa.
Automated Trading Algorithms: discord.gg/xuKHyhPKS6
Tutorials-YouTube: youtube.com/channel/UCJH8wJ8Ab_O-HTb0wrrtAKQ
Mathematical papers:
algoalert.net/pdfs/fourier.pdf
algoalert.net/pdfs/IEEEwavelet.pdf
Tutorials-YouTube: youtube.com/channel/UCJH8wJ8Ab_O-HTb0wrrtAKQ
Mathematical papers:
algoalert.net/pdfs/fourier.pdf
algoalert.net/pdfs/IEEEwavelet.pdf
Aviso legal
As informações e publicações não se destinam a ser, e não constituem, conselhos ou recomendações financeiras, de investimento, comerciais ou de outro tipo fornecidos ou endossados pela TradingView. Leia mais nos Termos de Uso.